The Insurmountable Problem of Formal Reasoning in Large Language Models

Good Morning,

Today we are going to talk about reasoning models and their capabilities. Anthropic the makers of Claude, have released this week a new ‘hybrid reasoning’ AI model. While OpenAI and others have released separate models focused on longer reasoning times, Anthropic adds advanced reasoning into standard models. Sort of like what OpenAI plans to do with a more unified GPT-5 later this year.

This is a guest post from of the Newsletter Mostly Harmless Ideas. I consider Alejandro a highly philosophical AI writer covering Op-Eds in a fairly satisfying manner. He’s a full-time college professor and researcher, working at the intersection between artificial intelligence and formal systems.

Mostly Harmless Ideas 🔬

Claude 3.7 Sonnet and Claude Code

Also more recently:

GPT-4.5 is Here

Anthropic > OpenAI in Reasoning Models

Claude 3.7 is an important moment in the history of “reasoning” models so it fits our topic today very well. This model is touted as the first hybrid reasoning AI model available on the market, blending both real-time responses and deeper reasoning processes into a single system. Anthropic has basically beaten OpenAI to this execution which says a lot about today’s ecosystem even though Claude is mostly a tool for Enterprise AI and B2B businesses, while ChatGPT is more popular among B2C consumers.

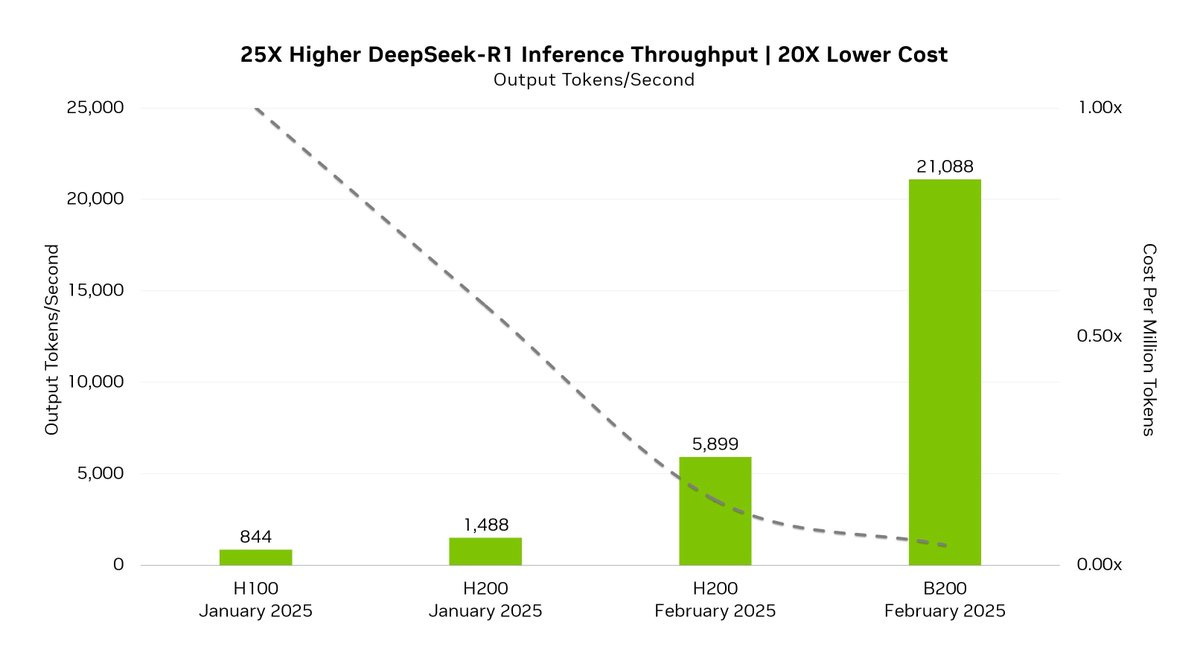
Nvidia recently released by the way, DeepSeek-R1 optimizations for Blackwell, delivering 25x more revenue at 20x lower cost per token, compared with NVIDIA H100 just four weeks ago. Fueled by TensorRT DeepSeek optimizations for Nvidia’s Blackwell architecture, including FP4 performance with state-of-the-art production accuracy, it scored 99.8% of FP8 on MMLU general intelligence benchmark.

Whether its OpenAI’s o3 model, DeepSeek, or Claude 3.7, reasoning models are part of the experiments of 2025 in AI and yet another frontier.

Alejandro is a double PhD in Machine Learning from the University of Alicante and the University of Havana, specifically in language modelling for the health and clinical domains. So we might want to take his opinions and enjoy his historical explorations seriously: (he is also fairly prolific)

• His general Substack: https://blog.apiad.net

• His Gumroad profile: https://store.apiad.net

• List of books he’s working on: http://books.apiad.net

• His link tree: https://apiad.net

As CoT becomes mainstream in our chatbots, Anthropic says the new model is capable of near-instant responses or extended responses that show step-by-step reasoning with users able to choose which type of response they’re looking for.

• Claude 3.7 Sonnet shows particularly strong improvements in coding and front-end web development. On February 10th, Anthropic released their Anthropic Economic Index that is super interesting. (Highly recommend you check it out – paper)

• Claude 3.7 Sonnet introduces a unique approach to AI reasoning by integrating quick response features with the ability to perform extended, step-by-step reasoning.

• Anthropic with the release is also introducing a command line tool for agentic coding, Claude Code.

• Meanwhile Perplexity has a new browser called Comet.

Top Articles by the Guest Contributor

Alejandro challenges us to think differently with some bold ideas:

• Why reliable AI requires a paradigm shift

• The Most Beautiful Algorithms Ever Designed

• Artificial Neural Networks Are Nothing Like Brains

• Why Artificial Neural Networks Are So Damn Powerful – Part I

Read more of his (top) work here.

We can Learn a lot from Anthropic’s Product Development about the Future 🚀

Launched on February 10, 2025, the Anthropic Economic Index aims to understand the impact of artificial intelligence (AI) on labor markets and the economy. Results:

• Today, AI usage is concentrated in software development and technical writing tasks.

• Over one-third of occupations (roughly 36%) see AI use in at least a quarter of their associated tasks, while approximately 4% of occupations use it across three-quarters of their associated tasks. Read more.

Claude 3.7 Sonnet is rolled out to all users and developers on Monday February 24th, 2025. Anthropic will likely acquire some of the best AI startups at the intersection of AI and software development. It’s so obvious. While Anthropic already powers AI coding tools like Cursor, it’s pitching Claude Code as “an active collaborator that can search and read code, edit files, write and run tests, commit and push code to GitHub, and use command line tools.”

Claude Code boasts a range of functionalities that streamline the coding process:

1. Code Understanding

2. Active Collaboration

3. Automation of Routine Tasks

4. Testing Support

Small Teams are the Future 💡

of Next Play made this infographic celebrating some of the AI startups that are scaling faster than usual with smaller than usual teams.

The Advent of Reasoning Models in 2025 🌊

Claude, (I mean AI) is indeed starting to rewrite the playbook for many AI startups, hilariously many of them powered by Anthropic. Important to note we can include Together AI in the above club. Read their guide on Prompting DeepSeek-R1. Now with better reasoning models, what will become possible? Claude 3.7 Sonnet has the same price as its predecessors: $3 per million input tokens and $15 per million output tokens—which includes thinking tokens.

While OpenAI’s ChatGPT is synonymous with Generative AI, it’s actually companies like Anthropic who are powering the future of Enterprise AI, along with companies like Cohere and others.

So this is all a segway to the very timely and relevant piece by Alejandro.

Subscribe to MHI

OpenAI Explorations 🗺️

If you are OpenAI fans, you have to check out a new series by of Generative Value:

1. OpenAI Part 1

2. OpenAI Part 2

3. OpenAI, Part 3: The (Probabilistic) Future of OpenAI

This is a very fulfilling deep dive today, especially suited for advanced reasons on AI, but it’s all made accessible by Alejandro, who currently lives in Cuba.

By January and February, 2025.

The Insurmountable Problem of Formal Reasoning in Large Language Models

Subtitle: Or why LLMs cannot truly reason, and maybe never will…

TL;DR: 🐇

• Large Language Models, at least in the current paradigm, have intrinsic limitations that prevent them from performing reliable reasoning.

• The stochastic sampling paradigm means hallucinations are irreducible, and some mistakes will always be possible.

• The bounded-computation architecture of Transformer-based LLMs means there are always problems that require more “thinking time” than any LLM can provide.

• Even with techniques like chain-of-thought prompting and integration with external tools, these limitations cannot be fundamentally overcome.

• Newer reasoning-enhanced models are a technical evolution but not a qualitative paradigm shift, so they are subject to the same limitations, even if diminished in practice.

• Ultimately, reliable formal reasoning in natural language might be unsolvable.

Reasoning models are the latest trend in AI.

Support independent authors who uncover glimpses of AI that the mainstream media cannot or will not, explore.

Go Premium

Listen on the Go 🌠 Audio version below: 40 minutes 37 seconds

It all began with OpenAI o1, a model designed to “think out loud” before arriving at answers, mimicking human thought processes in an almost uncanny way. Then came DeepSeek R1, which has garnered massive attention for its impressive performance in reasoning tasks, which sent shock waves across the whole AI industry and sparked a few conspiracy theories.

And now we’re seeing the upgrade from o1 to o3 in real-time (yes, these people are really bad at naming things), another reasoning model from China, and Google and Meta throwing their hats into the fight. Everyone is running to get their “reasoning” model out there as quickly as possible.

For many, these models seem to be more than just iterations of the previous paradigm; they represent a qualitative leap, particularly in tackling challenges that require logical reasoning. Across many difficult benchmarks, reasoning-enhanced models have shown impressive accuracy at the cost of increased response time, which seems like a fair deal.

The big shift is trading more computation during inference—making the model “think out loud” for, sometimes, several minutes before deciding on an answer—for a decreased rate of hallucinations and reasoning mistakes and an improved capacity for producing long chains of mostly sound logical arguments to arrive at a non-trivial (read, pattern-matched) answer.

However, despite their impressive performance, these models are not infallible. Numerous examples illustrate their limitations, where they deviate from the correct thinking path, arrive at incorrect conclusions, and even contradict themselves on occasion. In particular, these models seem to struggle with formal reasoning: mathematical and logical problems that require not as much real-world or common-sense knowledge but rather the precise application of logical inference rules.

This raises some crucial questions: Is the path to flawless reasoning merely a matter of superior data and extended training? Can we bridge the gap to achieve the kind of formal reasoning in natural language we’ve seen in sci-fi AIs—like Data from Star Trek or the hyperrational robots in Asimov’s narratives? Or is there something fundamentally limiting within the architecture of large language models that restricts their capability for comprehensive logical reasoning in natural language?

In this article, I will argue that LLMs have intrinsic limitations that hinder their reasoning abilities. The core of the argument boils down to the combination of stochastic language modelling with a fixed computational architecture, which renders LLMs incapable of provably correct general-purpose formal reasoning.

I will attempt to explain this in clear and intuitive terms and address the most compelling counterarguments to this perspective. This article summarises and expands on views I’ve expressed in several previous articles. It’s part of my ongoing attempt to understand where we are heading with LLMs regarding reasoning.

While much of this discussion in this article applies primarily to first-generation LLMs—anything before OpenAI o1—I will also explore how these fundamental constraints extend to newer reasoning-enhanced models. If my arguments hold, then nothing short of a novel paradigm can lead to AGI. In fact, I will argue that perfect reasoning from natural language may be computationally unsolvable, even in principle.

But before moving on, let me clarify something. I understand this topic is very controversial, and I know I will receive a lot of criticism, especially from some of the most ardent believers in the immediacy of AGI.

To be clear, I’m not claiming AGI is impossible. On the contrary, I’m firmly on the computationalist side here, and I believe machines can achieve the same and perhaps even superior levels of intelligence as any living, organic being. And I’m confident LLMs will play a significant role in the AGI breakthrough. That’s why I am among the many researchers working on better ways to make LLMs interact with other computational systems to enhance their capabilities. I’m just sceptical that all that’s left is throwing more GPUs and using the same techniques we already have.

With that out of the way, let’s explore what it means to say that LLMs are fundamentally limited in formal reasoning. This will be a long read, so buckle up!

What Do We Mean by Reasoning in LLMs

“Reasoning” is a very loaded term, that means a lot of things for different people—even for different groups of people who should agree on these definitions. So, I will attempt to define precisely what I mean by the phrase “LLMs cannot reason.”

In the Artificial Intelligence field, when we claim LLMs (or any computational system) can or cannot “reason”, we are, for the most part, not talking about any abstract, philosophical sense of the word “reason”, nor any of the many psychological and sociological nuances it may entail. There are many ways to define reasoning, from common sense to analogical to emotional to formal. In this article, I will focus on a precise, quantifiable, simplified notion of reasoning that comes straight from math.

Reasoning is, simply put, the capacity to draw logically sound conclusions from a given premise. Formal reasoning is when you follow a formalised method with hard rules to arrive at a conclusion. The most important tool for formal reasoning in math and science is logic, and it provides two fundamental reasoning modes: deduction and induction.

Induction is somewhat problematic for AI (and humans!) because it involves generalising claims from specific instances, and thus, it requires some strong assumptions. In contrast, deduction is very straightforward. It is about applying a set of predefined and agreed-upon logical inference rules to obtain new provably true claims from existing true claims. It is the type of reasoning that Sherlock Holmes is most famous for, and the thing mathematicians do all day long when proving new theorems.

Thus, in the remainder of this article, when I say “LLMs cannot reason”, I’m simply saying LLMs cannot perform logical deduction; that is, there are well-defined, computationally solvable deduction problems they inherently cannot solve. As I will attempt to convince you, this is not a value judgment or an informed opinion based on experience. It is a straightforward claim provable from the definition of deductive reasoning and the inherent characteristics of LLMs given by their architecture and functionality.

Now, if this definition of “reasoning” sounds like an oversimplification, well… in a sense, it is. I’m not addressing other forms of non-formal reasoning that are also paramount in human thinking, like abduction or common-sense and analogical reasoning. But formal reasoning, and particularly deductive reasoning, is the basis of mathematical and scientific research and crucial in informed decision-making, so any attempt to build an AI system useful for these tasks must be able to perform this mode of reasoning.

Before moving on to why LLMs cannot reason, let me address the most common counterargument I encounter whenever this topic is raised in non-academic contexts.

Can Humans Truly Reason?

Here is an argument you will hear a lot, and maybe even have made yourself:

“Sure, LLMs cannot really reason, but neither can humans, right? So what’s the big deal.”

I mean, humans can be stupendously irrational. We are prone to so many biases that, while useful in the biological and sociological context in which we evolved, in the modern world, are often more than not an obstacle to rational, logical thinking.

Despite this, the argument that since humans are not perfectly rational, it is OK for LLMs to also not be is flawed on many levels, so let’s unpack it.

First, while humans can make errors in reasoning, the human brain definitely possesses the capacity for open-ended reasoning, as evidenced by the more than 2000 years of solid math we have collectively built. Moreover, all college students—at least in quantitative fields—at some point have to solve structured problem-solving exercises that require them to apply logical deduction to arrive at correct conclusions, such as proving theorems.

So, while humans can be pretty stupid at times, we are certainly capable of the most rigorous reasoning when trained to do so.

But even more importantly, this assertion is a common case of whataboutism. Why does the fact humans can’t do something immediately make it OK for a piece of technology to fail at it? Imagine we did this with all our other tech. Sure, that aeroplane fell down and killed 300 people, but humans can’t fly. Or yes, that submarine imploded, but humans can’t breathe underwater. Or that nuclear power plant melted, but humans can’t stand 3000 degrees of heat, so what’s the big deal?

Obviously, we don’t do that. We compare any new piece of technology with our current best solution, and only if the new thing improves upon the old—at least on some metrics—do we consider the investment worthwhile. We replaced horses with cars because cars improved the previous best solution to individual transportation, at least on some fundamental metrics, if not all.

Granted, we often compare AI capabilities to human capabilities, but this is only because humans are the gold standard for the types of problems we often want AI systems to solve. So, we compare LLMs’ capacity to generate creative stories, engage in open-ended dialogue, or provide emphatic customer assistance with humans because humans are the best at these tasks.

However, there are well-established systems—such as traditional theorem provers—that excel in structured logical deduction and reasoning tasks. These systems are designed with rigorous validation mechanisms that ensure correctness and reliability in their outputs. They are basically flawless and incredibly fast.

So, in terms of the capability to perform purely logical, perfectly valid deduction, we already have a computational solution that sets the bar. Nothing short of provably correct deduction is good enough. The problem is these formal reasoning systems don’t understand natural language, of course, and that’s why we want LLMs to bridge the gap.

Why LLMs Are Incapable of Formal Reasoning

Let’s move on to the main limitations of current large language models that prevent general-purpose, provably correct deductive reasoning. I’m mostly thinking about LLMs implemented in the prevalent paradigm of the Transformer architecture, but these arguments apply to anything implemented using some sort of context-limited, probabilistic, sequential language model designed to run on GPUs.

The Argument from Stochastic Modelling

The first limitation of stochastic language models regarding reasoning is precisely their stochastic nature. These models generate outputs based on probabilistic predictions rather than deterministic logical rules. This means that even a well-structured prompt can and will yield different responses on different occasions due to the randomness of the sampling process.

Now, stochastic sampling is a necessary feature of LLMs, and not a bug. It is the fundamental reason that LLMs can produce varied, plausible, humanly-sounding text at all. It is also the only way we know how to capture in software, at least approximately, the many nuances and ambiguities of natural language.

That being said, stochastic sampling is a problem for deductive reasoning. For starters, an LLM might arrive at a wrong conclusion purely by chance, even if the right answer was the most likely continuation. This is, once again, the infamous problem of hallucinations.

To alleviate this, we may attempt to set the sampling temperature to zero, effectively forcing the model to fix the output for a given input. Thus, there will be no more different answers to the same prompt.

However, the underlying model is still probabilistic; we’re just greedily sampling the most likely continuation. The problem is that the mapping between input and output hinges on a probabilistic distribution that encodes correlations between elements in the input and corresponding elements in the output.

The reason this is problematic is simple: any probabilistic model of language that can generate new sentences that didn’t exist in the training data—that is, that can generalize at all—has to be, by definition, a hallucination machine. Or, to use Rob Nelson’s much better terminology: a confabulation machine.

You can think about it like this: if you want a language model to generate novel sentences, then it must be able to produce sentences it doesn’t really know, but somehow believes are correct. [1]

The way a stochastic language model “believes” a sentence is correct, is because the probability of seeing this exact sentence is high. Crucially, for novel sentences, this probability is high because there is some similarity to actual sentences in the training set.

This means any stochastic language model that’s useful at all needs to approximate correctness through plausibility. Sentences close (in a precise mathematical sense we won’t get into here) to what the LLM saw in the training set are thus considered correct. Sentences that are too dissimilar to anything in the training set are considered incorrect. But the frontier is fuzzy; there is no explicit threshold to distinguish what’s true from what’s not. All a stochastic language model can actually model is degrees of plausibility.

And there is the problem. Math and logic are not fuzzy [2]. There is no plausibility involved. A reasoning chain is either correct or incorrect. And more importantly, a tiny change in a single word—like adding a single “no” somewhere in a huge prompt—can completely shift the validity of a logical claim.

Whenever you approximate crisp mathematical correctness with fuzzy plausibility, you will have true and false claims close enough to each other such that a stochastic model cannot effectively distinguish them.

Now, this discussion has important nuances, so let’s analyse some interesting arguments about the role of randomness in reasoning.

Is Randomness a Bug or a Feature?

A common criticism of this argument regarding the stochastic nature of language models is that, in fact, randomness is essential in problem-solving and a crucial feature of many of the same SAT solvers I pretend to compare LLMs with. How hypocritical it is to posit randomness as a limitation when the most effective deductive reasoning algorithms are essentially random search algorithms!

This is true, but only partially, and it makes all the difference. So, let me explain.

Randomness plays a vital role in many computational problem-solving techniques, particularly in search algorithms for hard (read NP-complete or NP-hard) problems. Modern SAT solvers, for example, often employ randomized search strategies to efficiently explore vast solution spaces. By introducing randomness into the search process, these solvers can escape local optima and discover satisfactory solutions more quickly than deterministic methods might allow.

However—and here comes the crucial difference—using randomness in the search process does not imply that the entire reasoning process is inherently unreliable. Randomness is confined to the search phase of problem-solving, where it helps identify potential solutions—potential reasoning paths. However, once a candidate solution is found, a deterministic validation phase kicks in that rigorously checks the correctness of the proposed reasoning path.

This distinction between the search and validation phases is paramount in understanding how randomness contributes to effective problem-solving in general. During the search phase, algorithms may employ random sampling or other stochastic methods to explore possibilities and generate potential solutions. This phase allows for flexibility and adaptability, enabling systems to navigate complex landscapes of potential answers.

However, once a potential solution has been identified, it must undergo a validation process grounded in deterministic logic. This validation phase involves applying predefined, deterministic rules to confirm that the proposed solution meets all necessary criteria for correctness. As a result, any solution that passes this validation step can be confidently accepted as valid, regardless of how it was generated.

Here is a silly metaphor to illustrate this problem. If you sit a million monkeys in a million typewriters, at some point, one of them will randomly produce Romeo and Juliet. However, you need Shakespeare to filter the garbage out and decide which of the million pamphlets to publish.

What this means is randomness is good for exploring hypotheses but not for deciding which one to accept. For that, you need a deterministic, provably correct method that doesn’t rely on probabilities—at least if you want to solve the problem exactly.

However, in stark contrast to traditional problem-solving systems like theorem provers, LLMs lack a robust validation mechanism. While they can generate coherent and contextually relevant responses based on probabilistic reasoning, some of which may be correct reasoning chains, they do not possess a reliable method for verifying the accuracy of those outputs. The verification process is also stochastic and as subject to hallucinations as the generation process, rendering it effectively unreliable.

Therefore, since LLMs evaluate their own outputs using the same probabilistic reasoning they employ to generate them, there is an unavoidable, although perhaps small, risk that incorrect conclusions will be propagated as valid responses.

The monkeys are also the publishers.

The Argument from Bounded Computation

The second argument concerns the computational architecture of current language models. By design, LLMs spend a fixed amount of computation per token processed. Thus, the amount of computation an LLM does before it produces the first output token is a function of just two numbers: the input size and the model size.

So, if you ask an LLM to produce a yes or no question for a logical puzzle, all the “thinking” the model can do is some fixed—albeit huge—number of matrix multiplications that only depend on the input size.

Now, consider that you have two different logical puzzles with the same input size, i.e., the same number of tokens. But one is an easy puzzle that can be solved with a short chain of deduction steps, while the other requires a much higher number of steps. Here is the kicker: any LLM will spend exactly the same amount of computation on both problems. This can’t be right, can it?

A basic result in computational complexity theory is that some problems with very small inputs seem to require an exponentially high computational cost to be solved correctly. These are NP-complete problems, and most computer scientists believe there are no efficient algorithms to solve them. Crucially, a huge number of reasoning problems fall in this category, including the most basic logical puzzle of all—determining if a given logical formula can be satisfied.

When faced with an instance of an NP-complete problem, an LLM will produce an answer after a fixed amount of computation defined solely by the input size. Now, by sheer size, some larger models might just spend enough computation to cover many smaller instances of NP-complete problems.

As it happens, a huge constant function can be larger than an exponential function for smaller inputs. But crucially, we can always find instances of NP-complete problems that require, even in principle, a sufficiently large amount of computation to surpass the computational capacity of any LLM, no matter how big.

But this means something even more profound. Ultimately, LLMs are not Turing-complete systems but essentially very large finite automata. While they can handle a wide range of tasks and produce outputs that appear sophisticated, their underlying architecture limits the types of problems they can solve.

Turing completeness is the ability of a computational system to perform any computation given sufficient time and resources. Modern computers and many seemingly simple systems, such as cellular automata, are Turing complete systems. Ironically, LLMs are not.

The reason is simple. We know from computability theory that any Turing complete system must be able to loop indefinitely. There are some problems—some reasoning tasks—where the only possible solution is to compute, and compute, and compute until some condition holds, and the amount of computation required cannot be known in advance. You need potentially unbounded computation to be Turing complete.

And this is the final nail in the coffin. LLMs, by definition, are computationally bounded. No matter their size, there will always be problem instances—which we may not be able to identify beforehand—that require more computation than is available in the huge chain of matrix multiplications inside the LLM.

Thus, when LLMs seem to tackle complex reasoning problems, they often solve specific instances of those problems rather than demonstrating general problem-solving capabilities. This might just be enough for practical purposes—we may never need to tackle the larger instances—but, in principle, LLMs are incapable of truly open-ended computation, which means they are incapable of true reasoning.

But again, there is a lot of nuance in this limitation. For starters, this analysis applies very obviously to first-generation LLMs. But newer, so-called reasoning-enhanced LLMs work a little differently: they produce a potentially unbounded sequence of “thinking tokens” before deciding on the actual answer.

So, let’s examine this argument from the perspective of bounded computational power in more detail.

Can LLMs Perform Unbounded Computation?

A common counterargument is that LLMs can be rendered Turing complete by integrating them with external tools, such as code generators or general-purpose inference engines. Even easier is wrapping them in a recursive loop that can simply call the LLM as many times as necessary.

And this is true. You can trivially make an LLM Turing-complete, in principle, by duct-taping it with something that is already Turing-complete. You can also build a flame thrower with a bamboo stick, some duct tape, and a fully working flame thrower.

However, simply making LLMs Turing complete in principle does not guarantee that they will produce correct or reliable outputs. Integrating external tools or clever self-recursion introduces yet another layer of complexity and potential points of failure.

We need to address two main strategies in this regard: prompting and function calling. Let’s tackle them one at a time.

Prompt-based Techniques for Reasoning

Chain-of-thought prompting is the most basic way to increase the computation of LLMs. By guiding models to articulate intermediate reasoning steps before arriving at a final answer, CoT prompting helps decompose complex problems into manageable parts. This method has improved performance across various reasoning tasks, such as arithmetic and commonsense reasoning.

CoT makes the LLM “think harder” in that it forces the model to produce what we can consider “internal thought” tokens. Thus, we may view it as a way to perform additional computation on the input before deciding on the response.

This is precisely what modern reasoning-enhanced models like o1 and R1 are doing: automating the chain of thought prompt by baking it into the training process. However, despite its advantages, CoT prompting remains insufficient for several reasons.

On the one hand, CoT doesn’t address the fundamental limitation of hallucinations. The stochastic nature of LLMs means that even with CoT prompting, outputs can vary across different runs due to randomness in the generation process. This variability can lead to inconsistent reasoning outcomes, undermining the reliability of the model’s responses.

On the other hand, CoT extends the computation budget by a finite amount. To achieve true unbounded computation, we need a cyclic scheme in which the LLM is prompted to continue thinking, potentially indefinitely, until satisfied.

A potential solution for this problem is the intuitive approach of self-critique, which involves evaluating and refining an LLM’s responses with the same model, using prompts that instruct the model to read its previous output, highlight potential errors, and try to correct them. A form of after-the-fact chain-of-thought, if you might.

However, research also shows significant limitations in the effectiveness of this self-critique capability.

While LLMs can generate multiple ideas and attempt to critique their initial outputs, studies indicate that they cannot often meaningfully self-correct. Research also shows that self-correction techniques in LLMs are heavily contingent on the availability of external feedback. In many cases, LLMs perform better when they have access to an external verifier or additional context rather than relying solely on their internal reasoning capabilities.

And even more interestingly, attempts at self-critique can sometimes degrade performance rather than enhance it. Studies have shown that when LLMs engage in self-critique without external validation, they may generate false positives or incorrect conclusions. If you push harder, you can easily fall into a cycle of self-reinforcement of invalid or erroneous arguments, making the LLM increasingly more certain despite it getting worse and worse.

Ultimately, this circles back to the already discussed issue of relying on randomness for validation. If we attempt to get the model to tell us when it is certain it got the answer right, we are doomed. CoT and self-critique are great strategies for exploring different hypotheses and generating multiple possibilities, but they alone cannot reliably produce a provably correct conclusion all the time. [3]

Function Calling and External Tools

Integrating external tools, such as reasoning engines or code generation systems, into large language models represents a promising—and, for me, the only really viable—approach to enhancing their reasoning capabilities.

Connecting LLMs to external reasoning engines or logical inference tools makes it possible to augment their reasoning capabilities significantly. These tools can handle complex logical deductions, mathematical computations, or even domain-specific knowledge that the LLM might not possess inherently. Similarly, external code generation systems enable LLMs to produce executable code for specific tasks.

By leveraging these external resources, LLMs can potentially overcome some of their inherent limitations in logical reasoning and problem-solving. For starters, an external inference engine will be Turing-complete, so we scratch that problem down, right?

Not so fast. Unfortunately, this approach has many challenges, particularly regarding the LLM’s ability to generate the correct input for function calls or code execution. It all circles back to the original sin of LLMs: stochastic language modelling leads inevitably to hallucinations.

First, the effectiveness of function calling or code generation hinges on the model’s ability to interpret a task accurately and generate appropriate inputs. If the model misinterprets the requirements or generates incorrect inputs (e.g., if it hallucinates part of the inputs), the external tool will produce erroneous outputs or fail to execute altogether.

While external tools can, in principle, improve the reasoning capabilities of an LLM by providing structured logic and formal verification, they cannot compensate for LLMs’ basic limitations in generating reliable output. Therefore, there is no formal guarantee that the final output from this integration will be logically sound or appropriate for the context, simply because of the age-old adage: garbage in, garbage out.

How About Reasoning-Enhanced Models?

Finally, let’s briefly tackle what this means for state-of-the-art reasoning-enhanced LLMs, such as OpenAI’s o3 and DeepSeek R1. These models employ extended “thinking” phases during inference, where they generate multi-step reasoning chains, critique their own outputs, and iteratively refine conclusions. This approach reduces hallucinations and improves accuracy on benchmarks like mathematical problem-solving and logical puzzles, often outperforming earlier models by wide margins.

The mechanics of these enhancements are based on two key innovations. First is the chain-of-thought expansion, which allows models to explore branching reasoning paths for longer durations—sometimes minutes of computation—simulating deeper deliberation. Second, is the implementation of self-critique loops: internal validation mechanisms where the model evaluates its intermediate conclusions against problem constraints.

This article by Sebastian Raschka provides a much deeper and more technically detailed description of how these models work.

These techniques do improve practical performance by a large margin. It’s much better to bake CoT into the training process than simply relying on human-crafted prompts. During training, we can teach the model to automatically produce mostly correct reasoning chains by using formally verifiable training tasks, such as coding and math problems.

However, during inference, the accuracy of these models remains fundamentally limited by the probabilistic architecture of the underlying LLM. The self-critique process itself relies on the same stochastic language modelling that generates initial answers; there is no deterministic verification step during training. The same reliability issues remain, perhaps significantly decreased but not completely eliminated.

These models represent an evolution rather than a revolution. They scale up existing chain-of-thought techniques through increased computation and mirror human-like error checking with self-critique mechanisms that, ultimately, lack mathematical guarantees of correctness. Performance gains come from better exploring the model’s existing knowledge space rather than new reasoning capabilities.

So, despite the remarkable empirical improvements in reasoning-enhanced models, they are more a natural evolution of existing paradigms rather than a qualitative breakthrough. Their stochastic foundation ensures occasional failures will persist despite enhanced computing budgets. They are, indeed, very powerful tools for many real-world applications where absolute formal certainty is not required, but they cannot overcome their fundamental limitations when tasked with formal deductive reasoning tasks requiring strict accuracy guarantees.

Conclusions

The purpose of this article is to convince you of two claims:

1. Large Language Models currently lack the capability to perform a well-defined form of reasoning that is critical for important decision-making processes, including producing novel, scientifically valuable output.

2. We have absolutely no idea how to solve this in the near future within the prevalent and, so far, the only scalable language modelling paradigm.

This matters because there is a growing trend to promote LLMs as general-purpose reasoning engines. As more users begin to rely on LLMs for important decisions, to perform deep research on their behalf, and in domains where they cannot validate the results, the implications of these limitations become increasingly significant. At some point, someone will trust an LLM with a life-and-death decision, potentially with catastrophic consequences.

More importantly, the primary challenges in making LLMs trustworthy for reasoning are immense. Despite ongoing research and experimentation, we have yet to discover solutions that effectively bridge the gap between LLM capabilities and the rigorous standards required for reliable reasoning. Currently, our best efforts in this area are duct tape—temporary fixes that do not address the underlying limitations of the stochastic language modelling paradigm.

Now, I want to stress that these limitations do not diminish the many other applications where LLMs excel as stochastic language generators. In creative writing, question answering, user assistance, translation, summarization, automatic documentation, and even coding, many of the limitations we have discussed here are actually features.

The thing is, this is what language models were designed for—to generate plausible, human-like, varied, not-necessarily-super-accurate language. The whole paradigm of stochastic language modelling is optimized for this task, and it excels at it. It is much better than anything else we’ve ever designed. But when we ask LLMs to step outside that range of tasks, they become brittle, unreliable, and, worse, opaquely so.

The emergence of models like OpenAI’s o1 and o3 models, DeepSeek’s R1, Gemini 2.0, and the many more we’ll definitely see in the short term, seem like a significant step forward. And to a large extent, they represent innovative and creative approaches, and open up new avenues of research and applications.

However, we haven’t yet seen any fundamentally new paradigm in logical reasoning with LLMs. Deep down, this is “just” a way to explicitly incorporate chain of thought prompting in a fine-tuning phase and teach the model via reinforcement learning to select mostly coherent paths of deduction. It’s clever scaling of what already works fairly good, but not perfectly.

Thus, while definitely an impressive technical and engineering feat, these reasoning-enhanced models, and any future models based on the same paradigm, will continue to share the same core limitations inherent to all LLMs, only mitigated using some clever tricks. Hallucinations will still hamper any attempt at definitively solving formal reasoning with LLMs. It may be a matter of degree, and for some domains, good enough might just be good enough.

Ultimately, provably correct reasoning from natural language might even be an uncomputable problem. After all, natural language semantics are anything but formal, so going automatically from informal problem descriptions to formal, provably correct solutions might be impossible, even in principle. I have some ideas about why this may be the case, that I’ll share in a future article.

If I’m right, then maybe all we can hope for is a very clever, very efficient, never-tired, sometimes incorrect, not fully trustworthy AI assistant—less like Data and more like Bender minus the sarcasm. But we will never be able to completely remove expert human judgment from any life-or-death decision. And that might just be the best outcome.

What do you think?

Leave a comment

But for any loop that has a nonzero chance to stop at any given iteration, we can find a problem that requires stopping after a sufficiently large number of iterations, such that the probability the loop ends before required can be made as large as we want. That is, we can always find deduction problems for which the LLM cannot “think hard” enough, simply because there is a tiny chance it will “get tired” any given second. No matter how tiny, for large enough problems, the LLM will almost always fail to think hard enough.

About the Author

Bio: Alejandro Piad Morffis is a computer science professor and researcher at the University of Havana, Cuba, where he teaches at the Computer Science and Data Science majors, plus graduate courses in AI. He holds a double PhD in Machine Learning from the University of Alicante and the University of Havana, specifically in language modelling for the health and clinical domains. His primary research is about combining language models with formal methods to enhance their reliability and performance. He his father to two little girls. In his free time, he enjoys writing online about computer science and AI, as well as building open-source software on Github.

Editor’s Note

The arrival of DeepSeek-R1 on January 20, 2025 signaled the beginning of the reasoning model age of AI. No longer was OpenAI seen as the bleeding edge leader, but Google DeepMind, Claude and Chinese models made by the likes of DeepSeek and Qwen (Alibaba Cloud) had made significant progress over the last 9-12 months.

Reasoning models provide new quality capabilities for real-world application layer implementations.

DeepSeek released several distilled versions of the model, ranging from 1.5 billion to 70 billion parameters, broadening accessibility for various applications, making it a serious competitor in the AI landscape opening up a Pandora’s box of open-weight (open-source)’s impact on the AI ecosystem and opening up debate about China’s role at the future of application layer apps.

Reasoning models of 2025 are expected to produce new AI agentic capabilities that might impact Enterprise AI in a more tangible way. Anthropic, OpenAI and Google’s product timeline is therefore made a lot more interesting with tools like Deep Research (February 2nd), Operator (January 23rd) and so forth. Innovations by DeepSeek and their radical transparency might democratize AI in ways that mean China will be the future leader in open-source reasoning models.

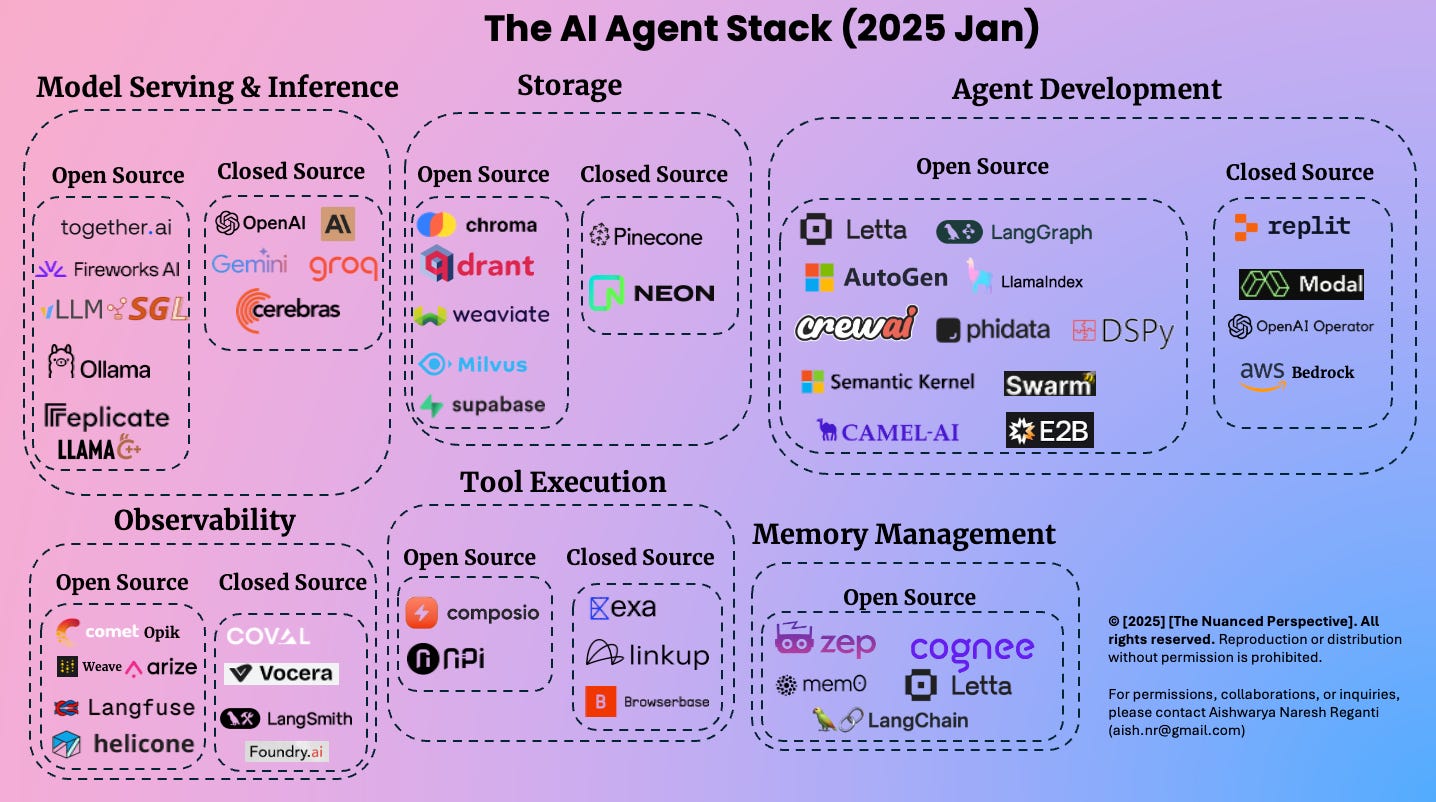
The AI Agent Stack, early 2025.

Infographic by , January, 2025.

Further Reading

Lastly important to note the gold standard on if LLMs can actually reason, please read Can Large Language Models Reason? by . (September, 2023).

Read More in  AI Supremacy